[新しいコレクション] y=x^2-4x-5 vertex 111588

Y = x2 − 4x − 5 y = x 2 4 x 5 Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 4 x − 5 x 2 4 x 5 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 4, c = − 5 a = 1, b = 4, c = 5 Consider the vertex form of a parabola Answer y = x² 4x 12 When y = 0 x² 4x 12 = 0 x² 4x 12 = 0 (x 2)(x 6) = 0 x = 2 or x = 6 The xintercepts are 2 and 6 y = (x² 4x) 12 yAnswer Vertex form of quadratic equation is => Y = a(X h)^2 k Let's simplify the given equation Add and subtract coefficient of X^2 on left side Y = 4X^2 8X 4 4 3 => Y = 4(X^2 2X 1) 4 3 => Y = 4(X 1)^2 1 So vertex of this parabola is V = (1,1)

Solution What Is The Equation Of The Axis Of Symmetry The Coordinates Of The Vertex Of The Graph Of Each Function For Y X 2 2x 5 Y X 2 4x 1 Y 2x 2 4x 2

Y=x^2-4x-5 vertex

Y=x^2-4x-5 vertex-Algebra Find the Vertex Form y=x^24x5 y = x2 4x − 5 y = x 2 4 x 5 Complete the square for x2 4x−5 x 2 4 x 5 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 4, c = − 5 a = 1, b = 4, c =Q What is the constant that should be added to the expression to complete the square x 2 16x Q What is the vertex of y=x 2 4x3?

2

1 To obtain the graph of y = (x 8)2, shift the graph of y = x2 2 To obtain the graph of y = x2 6, shift the graph of y = x2 A right, 8 B down, 6 A ball is thrown straight up from a height of 3 ft with a speed of 32 ft/s Its height above the ground after x seconds is given by the quadratic function y = 16x2 32x 3The axis of symmetry for the function f(x) = 2x2 4x 1 is the line x = 1 Where is the vertex of the function located?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

 To convert a quadratic from y = ax 2 bx c form to vertex form, y = a(x h) 2 k, you use the process of completing the square Let's see an example Let's see an example Convert y = 2x 2 4x 5 into vertex form , and state the vertexWhat is the vertex of the parabola y=2 (x3) 2 4 If given the equation y = 3 (x 5) 2 4, what is the vertex of the parabola? Change the quadratic equation y= x^24x5 from standard form to vertex form 1 Transpose the value to the left side of the equation 2 Complete the square of the expression on the right side of the equation to get a perfect square trinomial Add the resulting term to both sides

There are no real x intercept solutions This parabola opens upward with a vertex above the x axis y = x^2 4x 5 0 = x^2 4x 4 4 5 y = (x 2)^2 1 demonstrating that the vertex is (2, 1) hence above the x axis 924 viewsIn the conic section, the vertex form of a parabola is a point or place where it turns, it is also known as a turning point If the quadratic function converts to vertex form, then the vertex is (h, k) The vertex equation is y = a(x– h)2 kGiven y= 8x^2 4x 3 We need to find the vertex We know that a= 8 b= 4 c = 3 Let V be the vertex such that V (xv, yv) xv = b/ 2a ==> 4/2*8 = 4/16 = 1/4

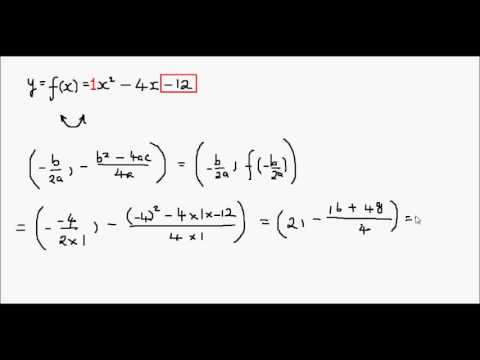
How To Sketch A Parabola Example 2 Y X 2 4x 12 Youtube

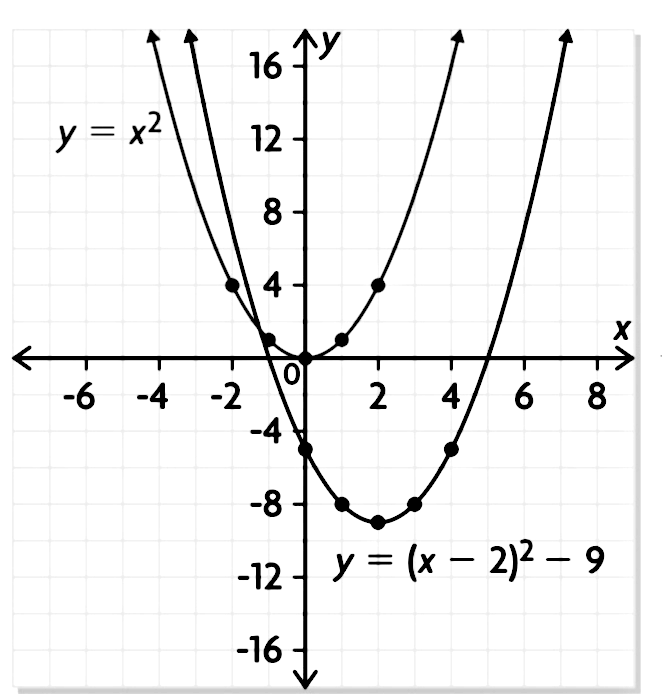
Y X 2 4x 5 Snapsolve

Find the range and domain and vertex and intercepts of a graph whose parabola is x^24x5 Standard form of parabola y= (xh)^2k, with (h,k) being the (x,y) coordinates of the vertex y=x^24x5 completing the squareAnswers The general equation of a quadratic is expressed as y = ax^2bxc To convert the general equation to vertex form, we need to obtain this form (y k)= a (x h)^2 This could be done by using completing the square method y = –3x^2 – 12x – 2 y 2 = –3 (x^2 4x)Given the parabola with standard equation {eq}y=x^24x5 {/eq} Then {eq}a=1, b=4, c=5 {/eq} Find the vertex using the vertex formula {eq}\begin{align} h&=\dfrac

Solution Solve By Vertex Form Y X 2 6x 12 Y 4x 2 24x 11

1

 The vertex form of a quadratic function is given by y = a(x − h)2 k, where (h,k) is the vertex of the parabola We can use the process of Completing the Square to get this into the Vertex Form y = x2 − 4x 2 → y −2 = x2 − 4x (Transposed 2 to the Left Hand Side) Now we ADD 4 from each side to complete the square → y −2 4 = x2 − 4x 22 Methods for solving quadratic equations We find the vertex of a quadratic equation with the following steps Get the equation in the form y = ax2 bx c Calculate b / 2a This is the xcoordinate of the vertex To find the ycoordinate of the vertex, simply plug the value of b / 2a into the equation for x and solve for yA quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabola

Solution What Is The Equation Of The Axis Of Symmetry The Coordinates Of The Vertex Of The Graph Of Each Function For Y X 2 2x 5 Y X 2 4x 1 Y 2x 2 4x 2

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Given an equation in vertex form, such as y = 4(x 3) 2 4, we can convert this to the standard form simply by multiplying the binomial and simplifying y = 4(x 3) 2 4 y = 4(x 2 6x 9) 4 y = 4x 2 24x 36 4 y = 4x 2 24x 40 So, the equation, y = 4(x 3) 2 4 and the equation y = 4x 2 24x 40 are the same, except inVertex\(y3)^2=8(x5) vertex\(x3)^2=(y1) parabolavertexcalculator vertex y=2x^{2}4x12 en Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowingAnswer (1 of 11) Graphical Solution ANSWER These curves have very practical uses but it takes time for them to become friends for you Note the crossing of the y axis and the 5 constant term in the equation in this form Completing the square gives you the coordinates of the vertex Solvin

Roots With Calc2

Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download

Y = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, ySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSubtract y from both sides x^ {2}4x4y=0 x 2 4 x 4 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and 4y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0 Substitute 1 for a, 4 for b, and 4 − y for c in the quadratic

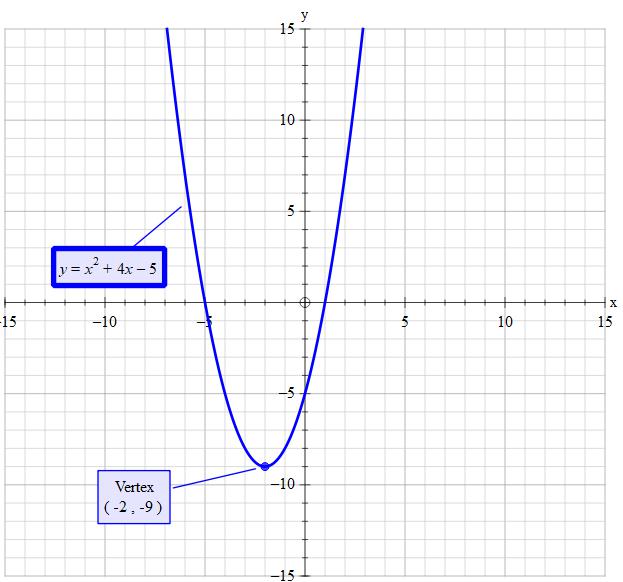
The Axis Of Symmetry For A Function In The Form F X X 2 4x 5 Is X 2 What Are The Coordinates Of The Vertex Of The Graph Socratic

Solution 2 For The Function Y X2 4x 5 A Put The Function In The Form Y A X H 2 K B What Is The Equation For The Line Of

When y = a*x^2 b*x c, the xcoordinate of the vertex is b / (2a) The xcoordinate of the vertex of this parabola is (10) / (2*(1)) = 5 y = (5)^2 10*(5) 2 = 502–25 = 27 Vertex is the point (5, 27)Find the Vertex y=x^28x5 Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side f(x) = 6x^24x5 find the vertex axis of Symmetry xintercepts yintercept value of the max/min domain range of the following quadratics and then g raph the parabola the distance between johns house and alberts house is 8 1/3 miles a park is located on a straight path between the two houses if the park is 3 4/5 mi

3 2 Quadratic Functions Mathematics Libretexts

How To Rewrite A Quadratic Function To Find Its Vertex And Sketch Its Graph Algebra Study Com

Q Write y = x 2 4xLet's graph y=x 2 (blue), y=¼x 2 (green), y=½x 2 (purple), y=2x 2 (red), and y=4x 2 (black) on the same axes For all these positive values of a , the graph still opens up Notice when 0< aAnswer by lwsshak3 () ( Show Source ) You can put this solution on YOUR website!

2

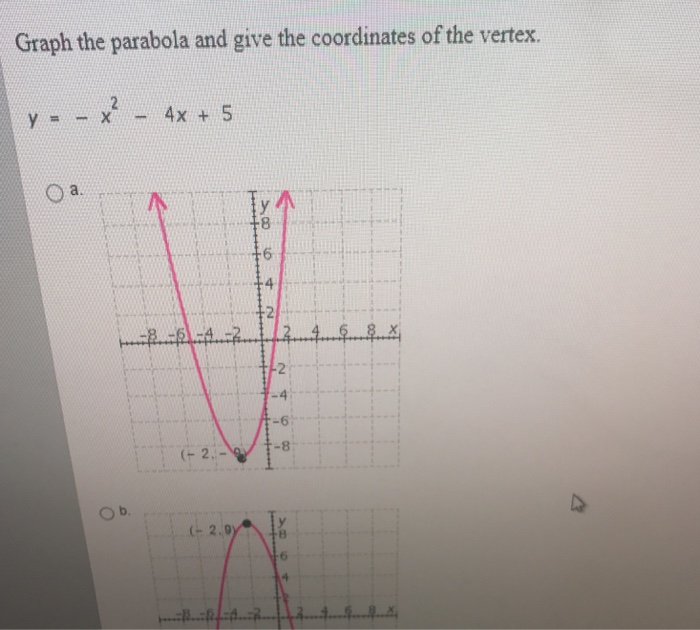
Solved Graph The Parabola And Give The Coordinates Of The Chegg Com

 Write y = x2 − 4x − 1 in vertex form y = (x − 2)2 5 y = (x − 2)2 − 5 y = (x 2)2 5 y = (x 2)2 − 5 1 See answer creepycrepes is waiting for your help Add your answer and earn points kelcey93 kelcey93 Y=(52)5x2 367 7942 x 50 whhhuuu New questions in MathematicsSal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabola that as well so all right that is 5 times x squared minus 4x and then I have this 15 out here 15 out here and I want to write this as a perfect square and we just have to remind ourselves that if Given `y=x^26x5` The vertex will be the minimum value of this function (the graph is a parabola opening up), and the axis of symmetry is the vertical line through the vertex

Given The Function ƒ X X 2 4x 5 Identify The Zeros Using Factorization Draw A Graph Of The Brainly Com

Solution Graph F X X 2 4x 3 Labeling The Y Intercept Vertex And Axis Of Symmetry

We are given the function {eq}y=5x^24x3 {/eq} We want to know the vertex of the given function So, we have Solution The graph of the given The xcoordinate of the vertex is halfway between the xintercepts, so can be found by averaging their values vertex xcoordinate = (1 5)/2 = 2 The ycoordinate of the vertex is the value of y for that value of x y = (2 5)(2 1) = (3)(3) = 9 filling x=2 into the factored equation The vertex is (x, y) = (2, 9) _____By signing up, you'll get thousands

Ch 5 Notes Ppt Video Online Download

Solution Use The Graph Of Y X2 4x 5 To Answer The Following A Without Solving The Equation Or Factoring Determine The Solution S To The Equation 4 5 0 2 X Amp 614 Amp X

Answers 2 Get Other questions on the subject Mathematics Mathematics, 1810, kidzay If aDivide 4, the coefficient of the x term, by 2 to get 2 Then add the square of 2 to both sides of the equation This step makes the left hand side of the equation a perfect square Square 2 Add y1 to 4 Factor x^ {2}4x4 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2}Subtract y from both sides Subtract y from both sides x^ {2}4x5y=0 x 2 4 x − 5 − y = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

For A Quadratic Function Find Vertex Axis Of Symmetry Domain And Range Intercepts Youtube

(0, 1) (1, 3) (1, 7) (2, 1)Functionvertexcalculator en Related Symbolab blog posts Functions A function basically relates an input to an output, there's an input, a relationship and an output For every inputWhere the curve of x^2 4x 5 = 0 intercepts the yaxis, x = 0 Here we see that (4)^2 < 4*a*c, the curve does not intersect the xaxis The yintercept is (0, 5) We need to find y and x

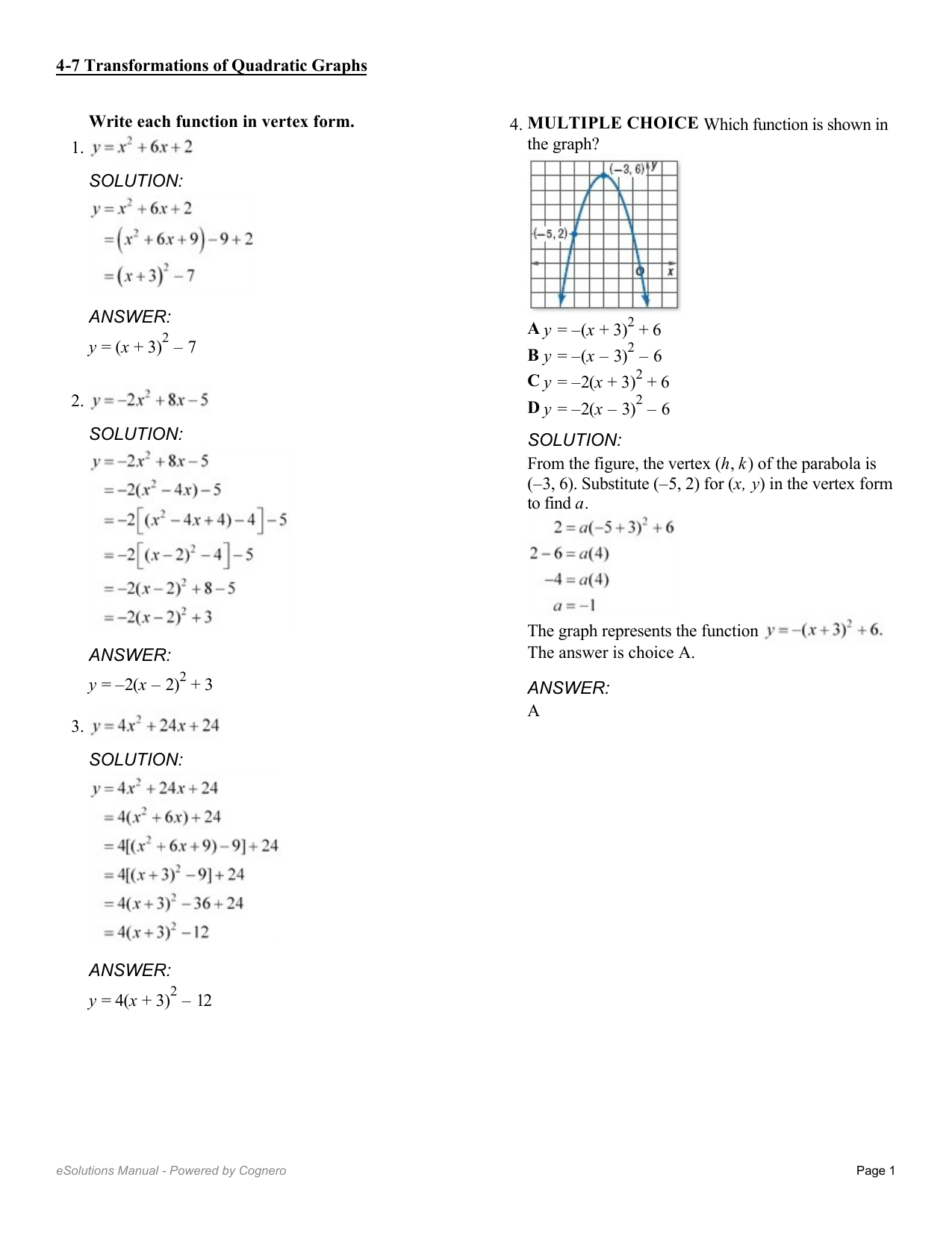
Write Each Function In Vertex Form 1 Solution Answer Y X

Solution Graph F X X 2 4x 5

Answer to How do you graph the parabola y = x^2 4x 3 using the vertex, intercepts, and additional points?Algebra Graph y=x^24x5 y = x2 4x − 5 y = x 2 4 x 5 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 4 x − 5 x 2 4 x 5 The quadratic equation is y = x^2 4x 5 how do i find the The quadratic equation is y = x^2 4x 5 how do i find the vertex and do the number line ?

3 Vertex Form

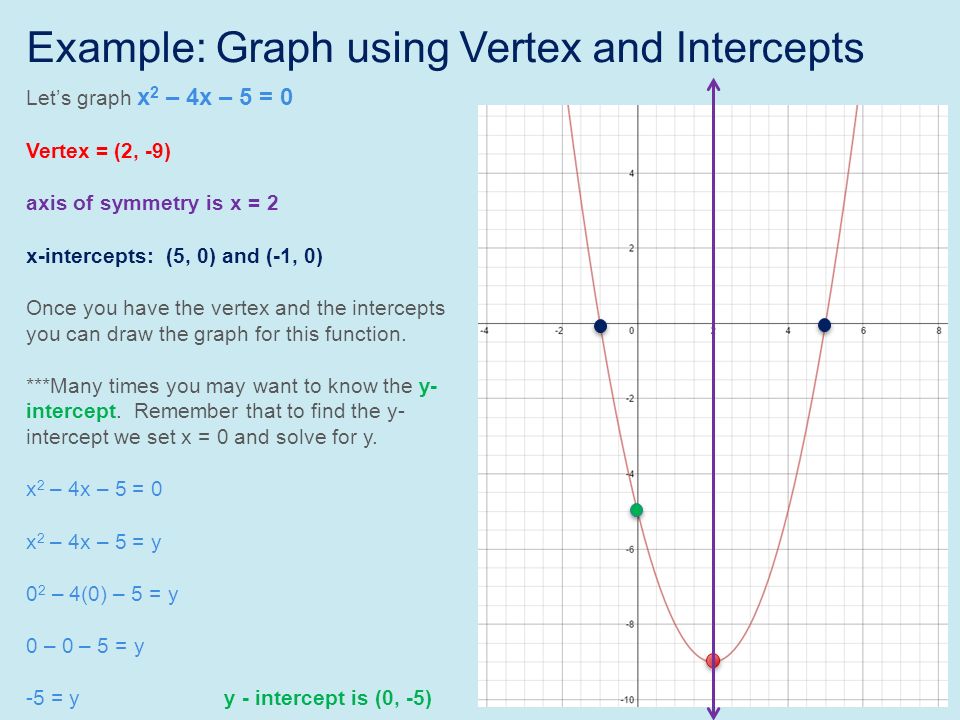
More Key Factors Of Polynomials Recall From Lesson 4 Standard Form Left To Right Factored Form The Fta Fundamental Theorem Of Algebra States That Ppt Download

Answer (1 of 3) What is the vertex of the parabola y = x^2 10x 2?Find the Vertex Form y=x^24x Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of and

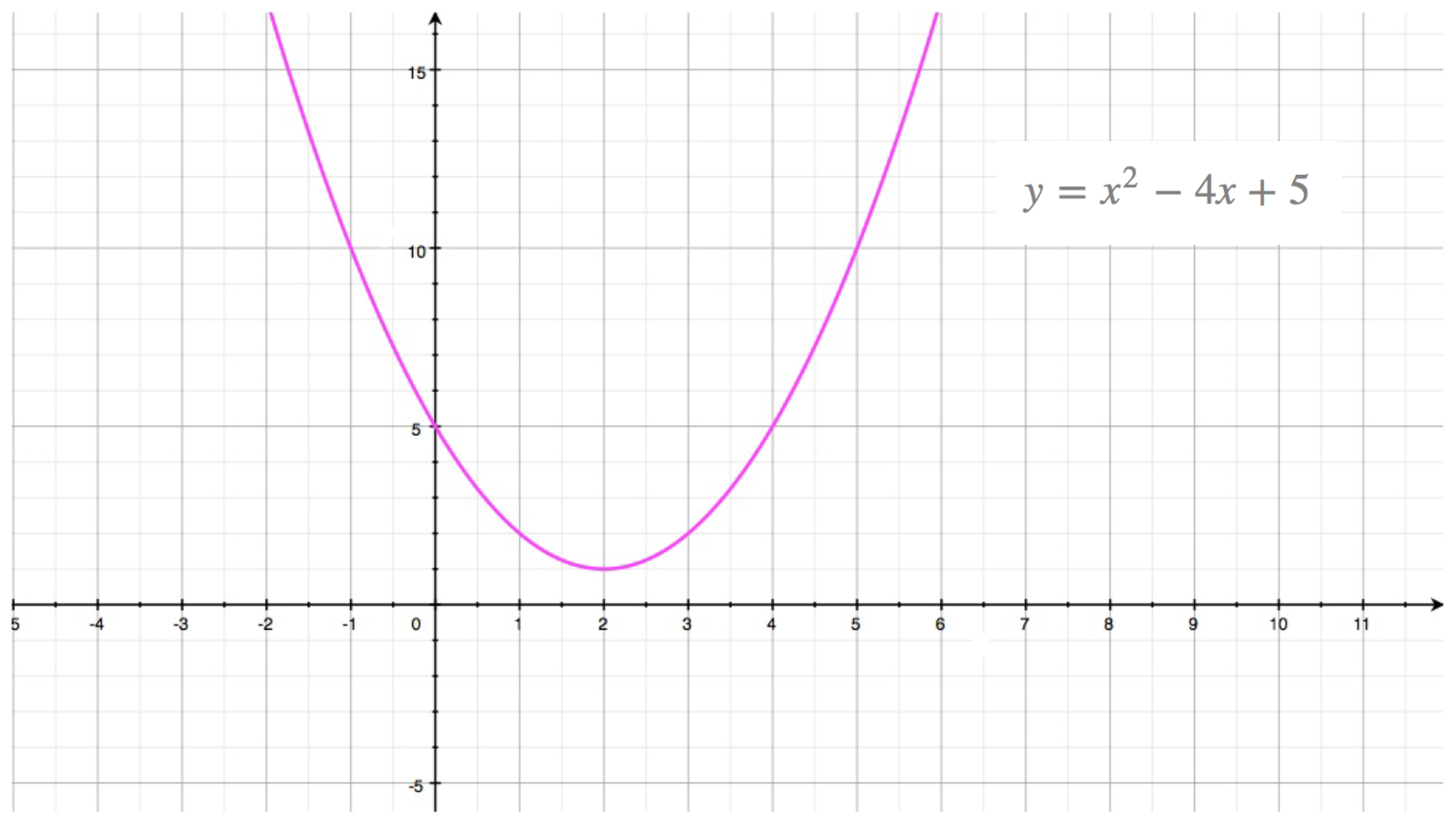
Quadratic Function Parabola

Solved Suppose That F X X 2 4x 12 What Is The Vertex Chegg Com

Y Classzone

Solved Solve For X And Simplify The Answer A 6x2 2x 3 0 B Chegg Com

Plot A Graph For The Equation Y X 2 4x 1

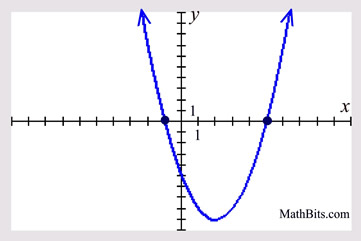
Quadratic Graph Practice Mathbitsnotebook A1 Ccss Math

Solution Please Help Use The Graph Of Y X 2 4x 5 To Answer The Following Using The Graph What Are The Solution S To The Equation X 2 4x 5 0 Does This Function Have A Maximum Or A Mini

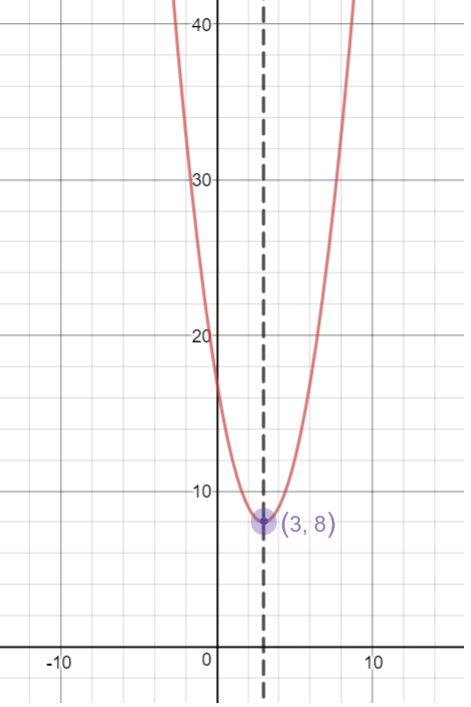
Vertex Form Of A Quadratic Equation Algebra Socratic

Solution Using The Graph Of Y X 2 4x 5 What Is The Equation Of The Line Of Symmetry For This Graph

The Standard Form Of The Equation Of A Parabola Is Y X 2 4x 22 What Is The Vertex Form Of The Brainly Com

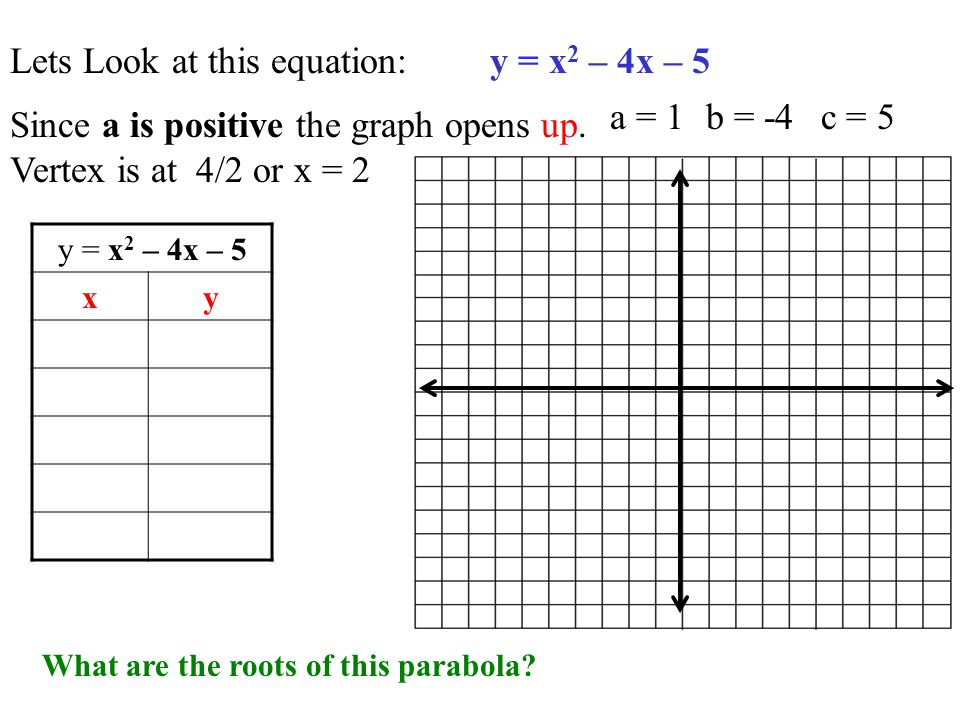
Y X 2 2x 8 Xy Vertex Max Or Min Axis Of Symmetry Do Now 4 From Classwork Ppt Download

Solution Use The Graph Of Y X 2 4x 5 To Answer The Following Determine The Solution S To The Equation X 2 4x 5 0

Graph The Parabola Y X 2 4x 1 Youtube

2 02 Quadratic Equations

Regents Review 3 Functions Quadratics More Ppt Video Online Download

Complete The Square To Rewrite Y X2 4x 5 In Vertex Form Then State Whether The Vertex Is A Brainly Com

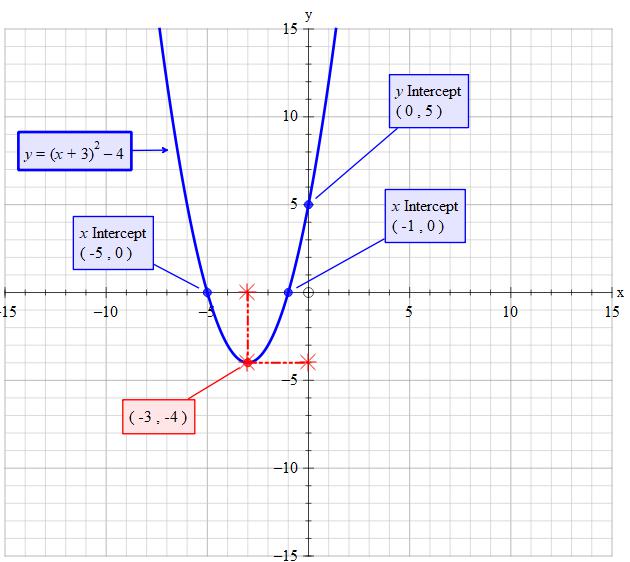
How Do You Find The Vertex And Intercepts For Y X 3 2 4 Socratic

X2 4x 5 0

How To Find The Vertex Of A Quadratic Equation 10 Steps

Answered For The Function Y X2 4x 5 Find The Bartleby

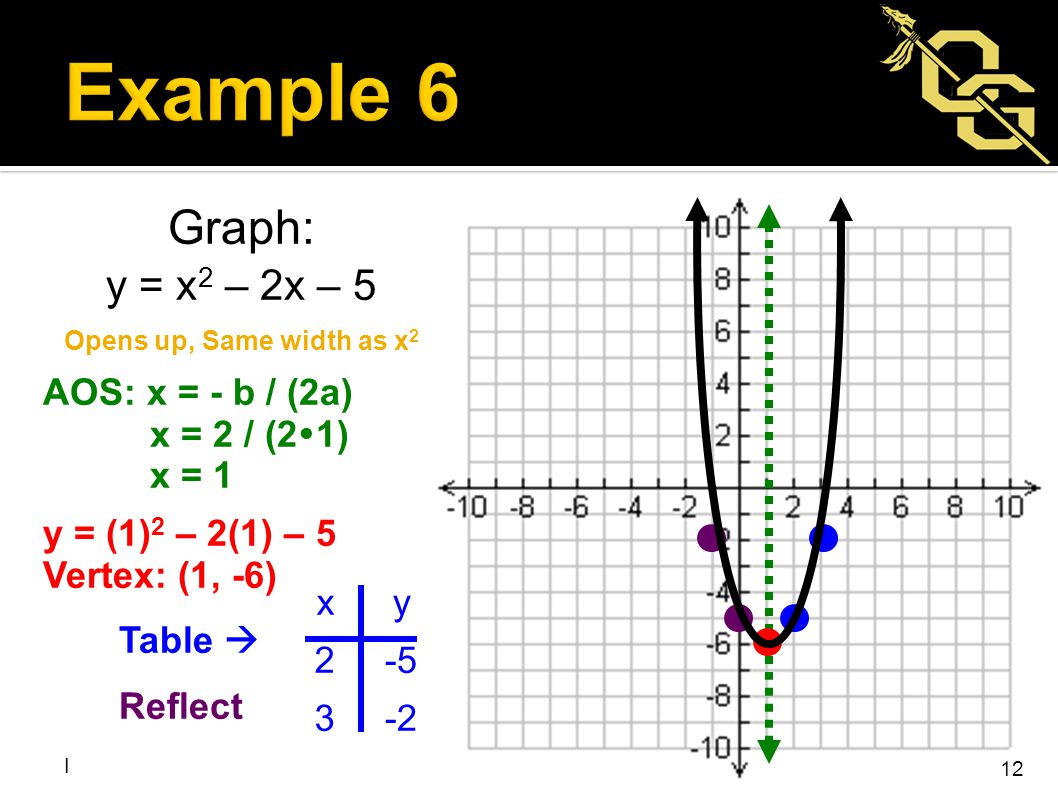
Example 6 Write A Quadratic Function In Vertex

What Are The Vertex And X Intercepts Of The Graph Of Y X2 4x 21 Select One Answer For The Vertex Brainly Com

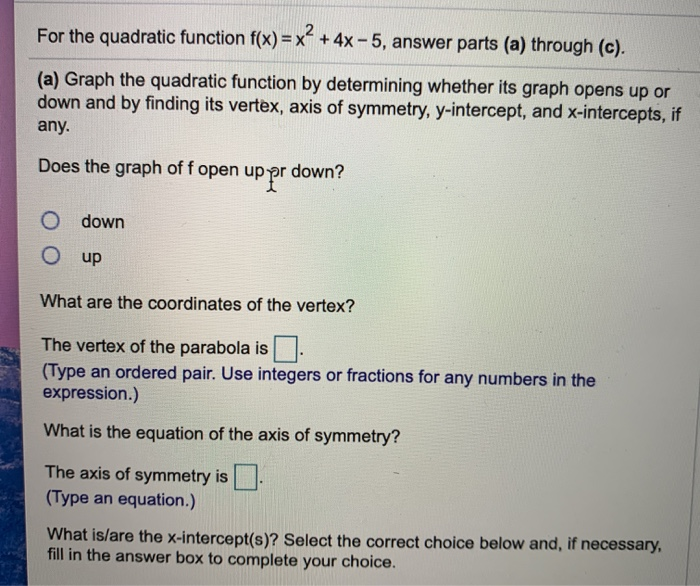
Solved For The Quadratic Function F X X 4x 5 Answer Chegg Com

Given Function F X X2 4x 5 Determine The Vertex Axis Of Symmetry Calculate Y Intercept Find Additional Point On Graph Graph Function Submit Graph Enotes Com

Quadratics Graphing Parabolas Sparknotes

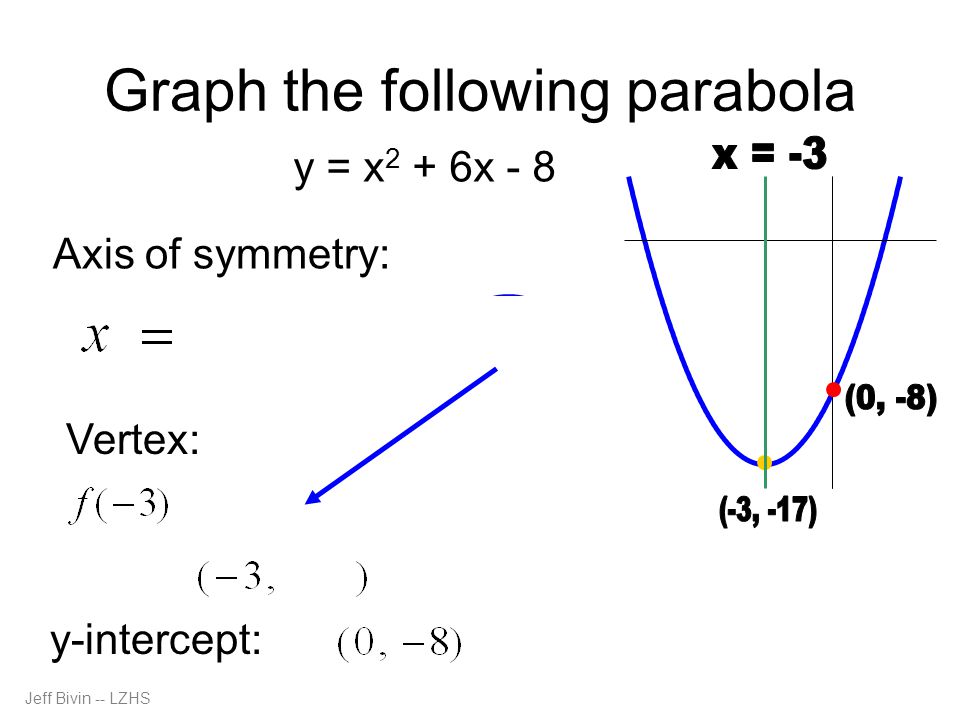
Graphing Parabolas Using The Vertex Axis Of Symmetry Y Intercept By Jeffrey Bivin Lake Zurich High School Last Updated October Ppt Download

2

Unique Quadratic Equation In The Form Y Ax 2 Bx C

Y 3x 2 6x 5 Graph On Coordinate Plane Mathskey Com

Solved Given Y X 2 4x 5 A Find The X And Chegg Com

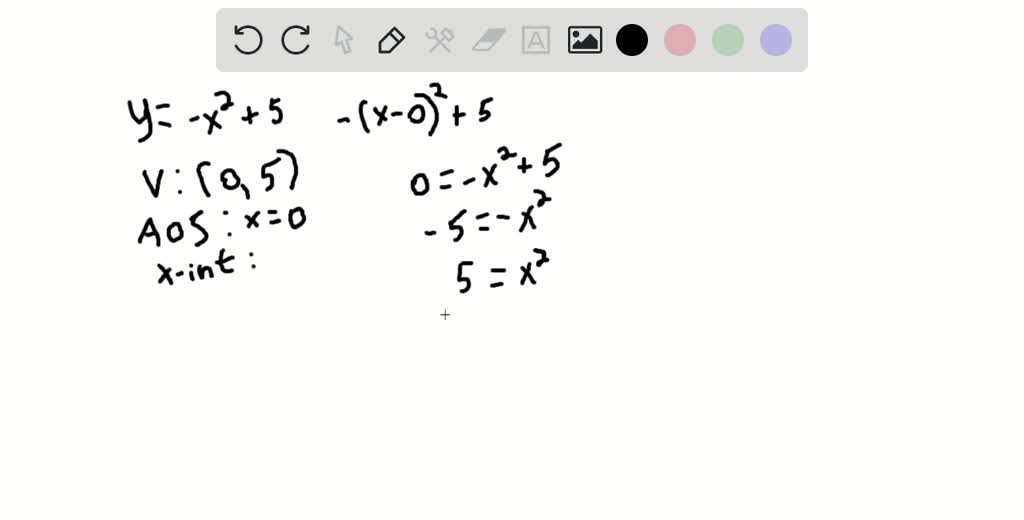
Solved For The Quadratic Equation State The Axis Of Symmetry Vertex And Any Intercept Y X 2 4x 5 Axis Of Symmetry Vertex X Y Y Intercept X Y

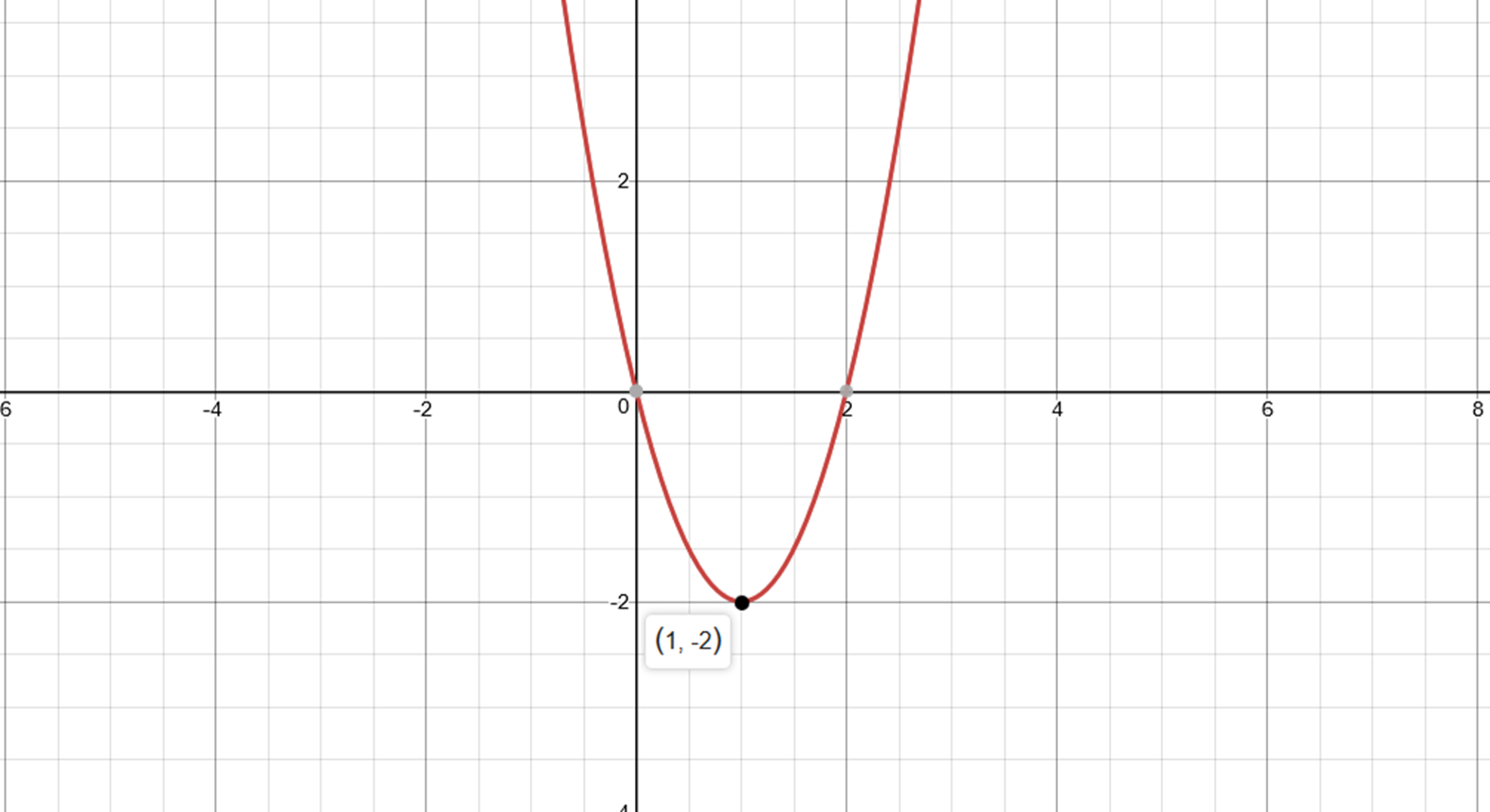
How Do You Find The Vertex Of Y 2x 2 4x Socratic

2

Ay U 3 Use The Vertex And Intercepts To Sketch The Graph Of The Quadratic Function Homeworklib

2

5 3 The Graphs Of Quadratic Equations X

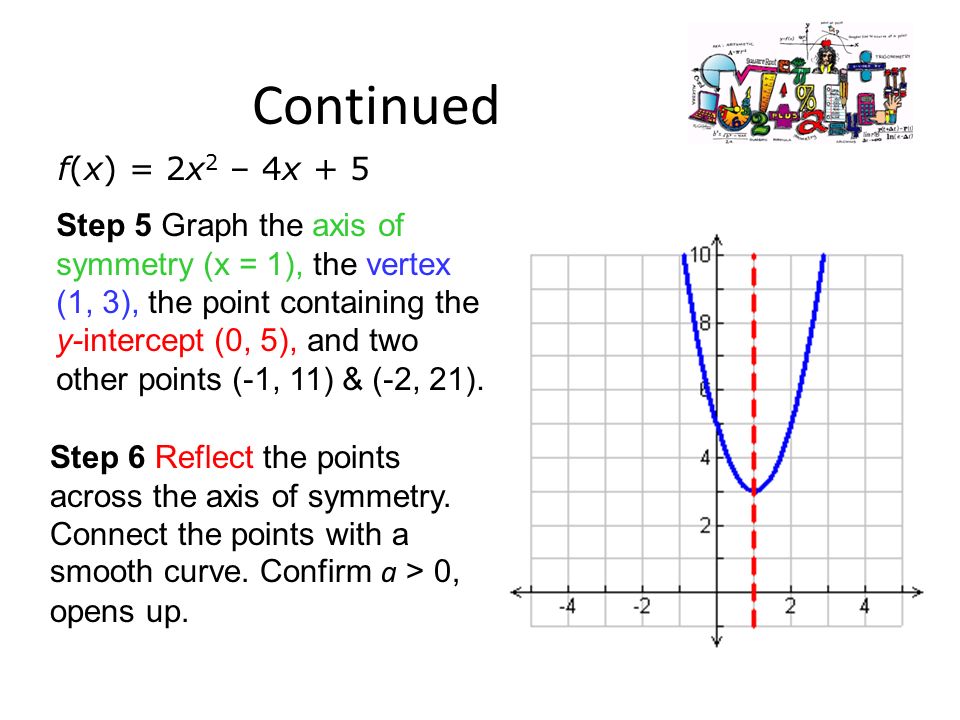
Algebra 2 Standard Form Of A Quadratic Function Lesson 4 2 Part Ppt Download

Y X 2 4x 32 Axis Of Symmetry 2 Vertex 2 36 X Intercepts 4 0 8 0 How Dose The Axis Of Symmetry Relate To Enotes Com

The Function Y X 2 4x 5 Approximates The Height Y Of A Bird And Its Horizontal Distance X Brainly Com

Vertex Form Vertex Form Vertex Form Is Another

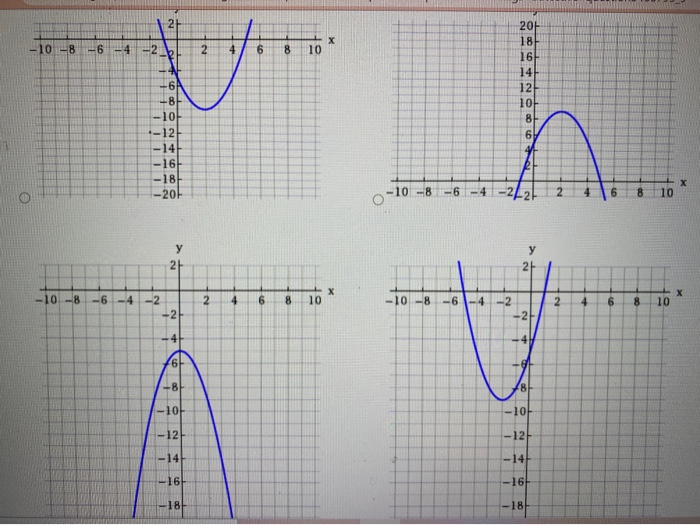
Solved For The Quadratic Equation State The Axis Of Chegg Com

1

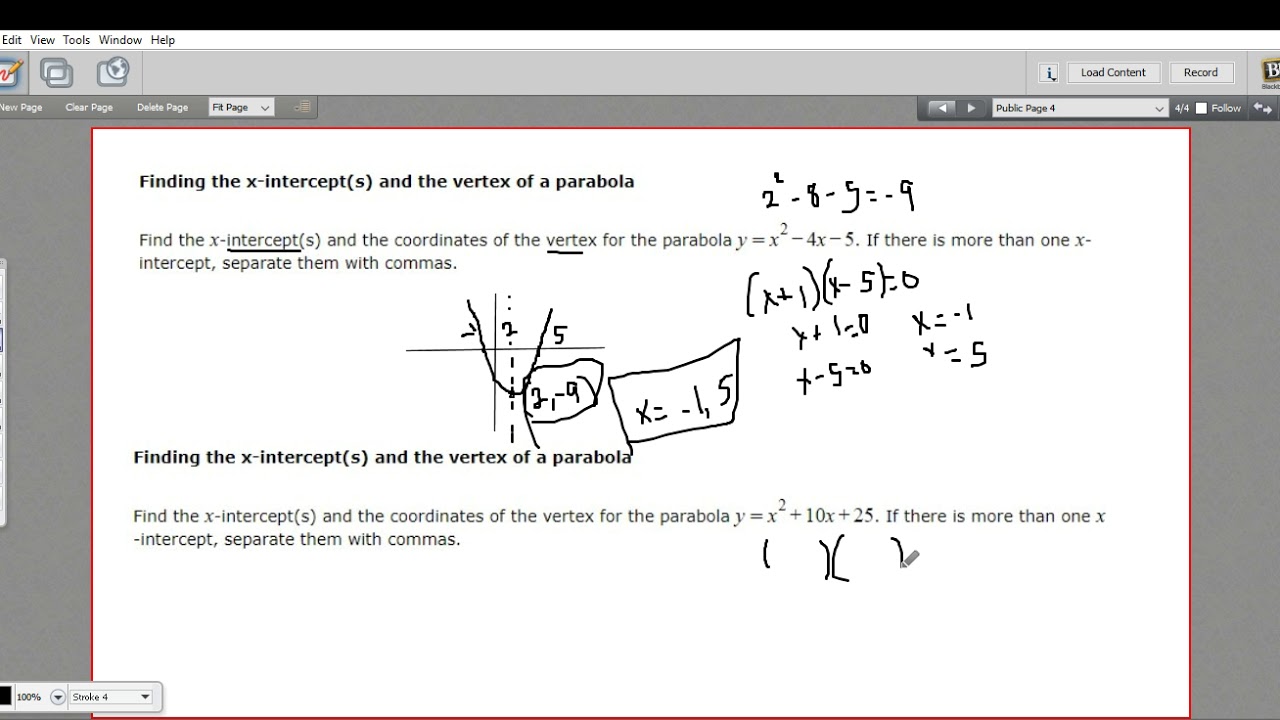
Finding The X Intercepts And Vertex Of A Parabola Youtube

The Quadratic Equation Is Y X 2 4x 5 How Do I Find The Vertex And Do The Number Line Brainly Com

Identify The Vertex Of Y X2 4x 5 Brainly Com

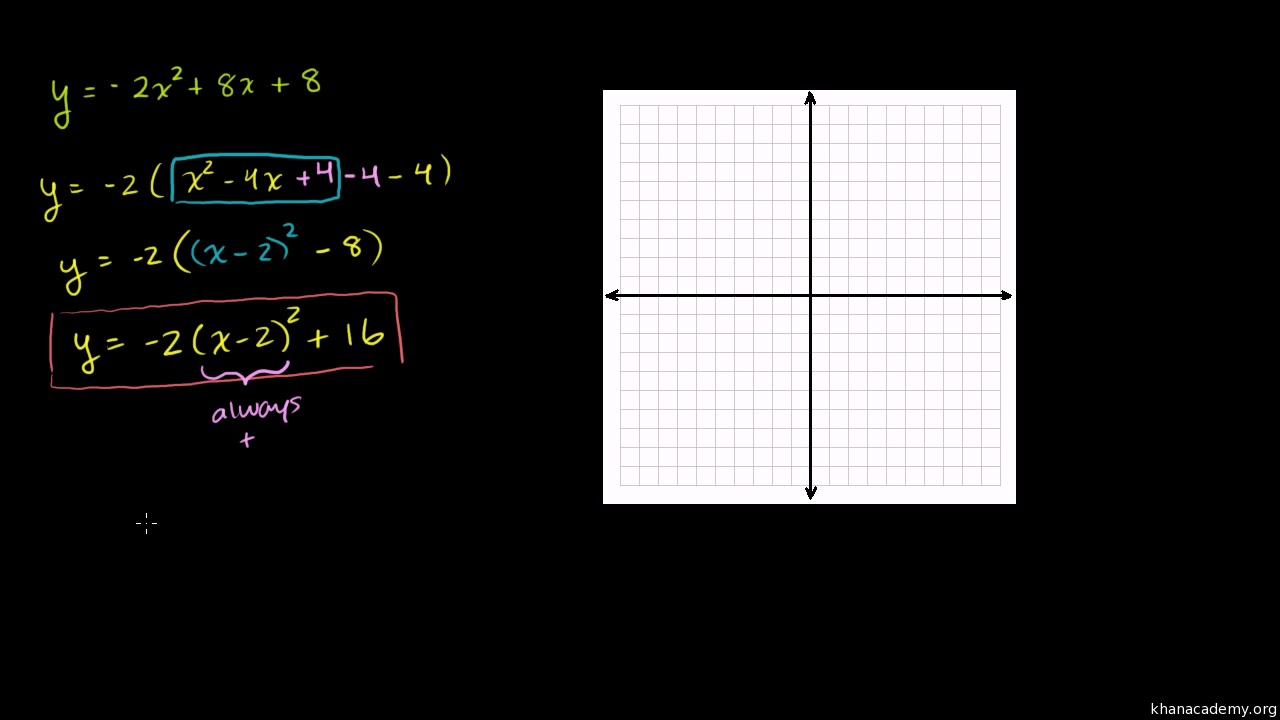
Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

4 7 Write In Vertex Form

2

Y X2 4x 6 Math Homework Answers

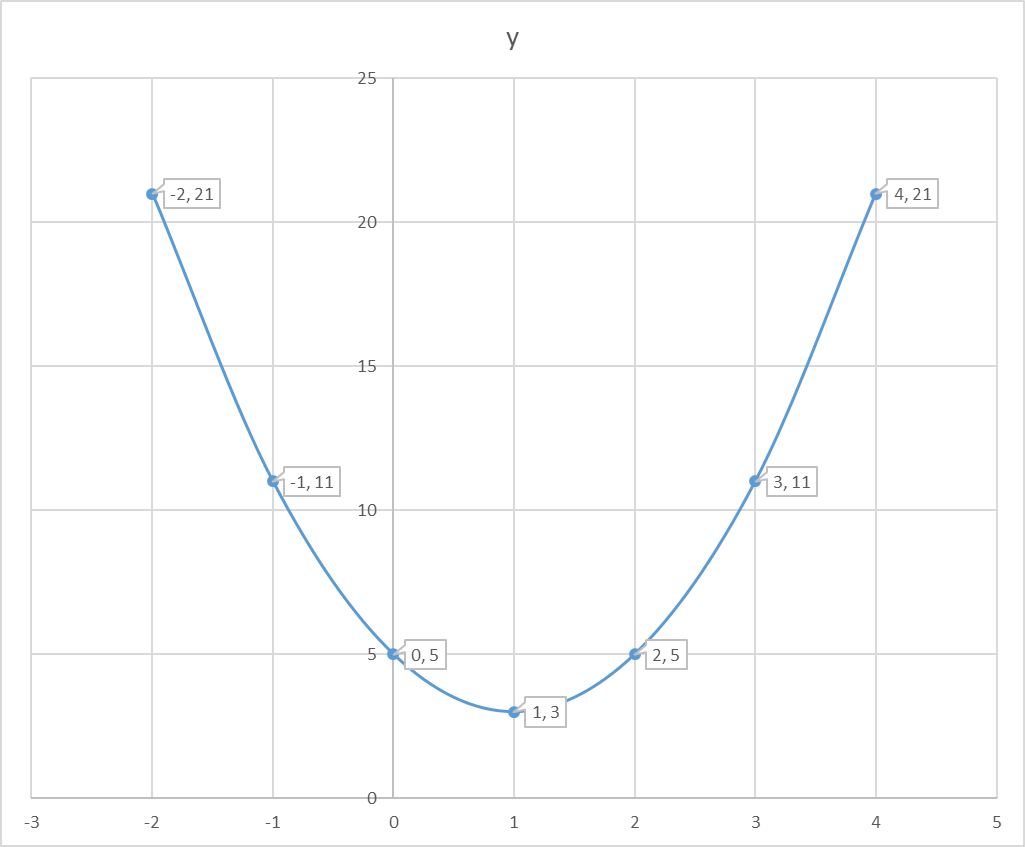
How Do You Graph The Parabola Y 2x 2 4x 5 Using Vertex Intercepts And Additional Points Socratic

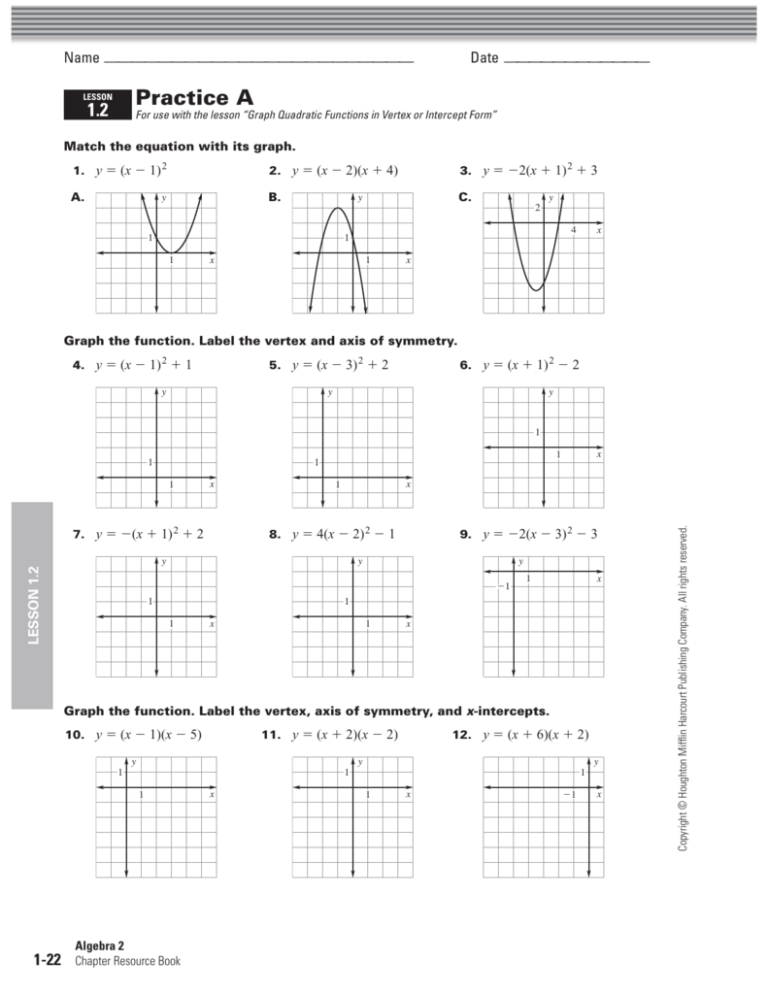
Practice 1 2 Graphing In Vertex Form And Intercept Form

What Is The The Vertex Of Y X 2 4x Socratic

Quadratics Review 1 Quadrtics Test Review 1

Solution Can You Graph The Equation Y X 2 4x 5 If You Can Please Explan How U Got The Vertex And How To Graph Everything Thanks

Completing The Square Solving Quadratic Equations 1 Express The Followings In Completed Square Form And Hence Solve The Equations X 2 4x 12 0 X Ppt Download

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

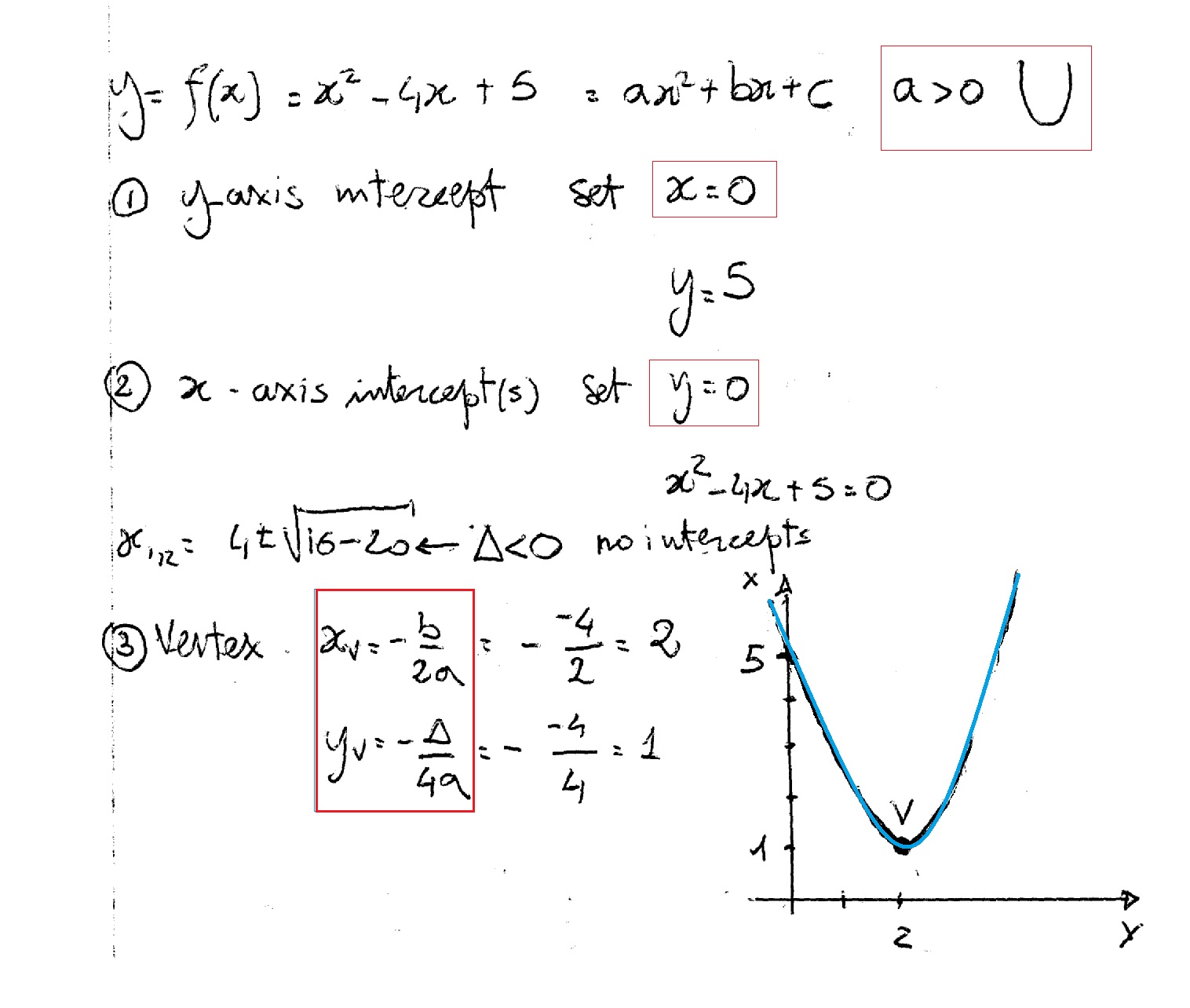
How Do You Graph F X X 2 4x 5 Socratic

Characteristics Of Parabolas College Algebra

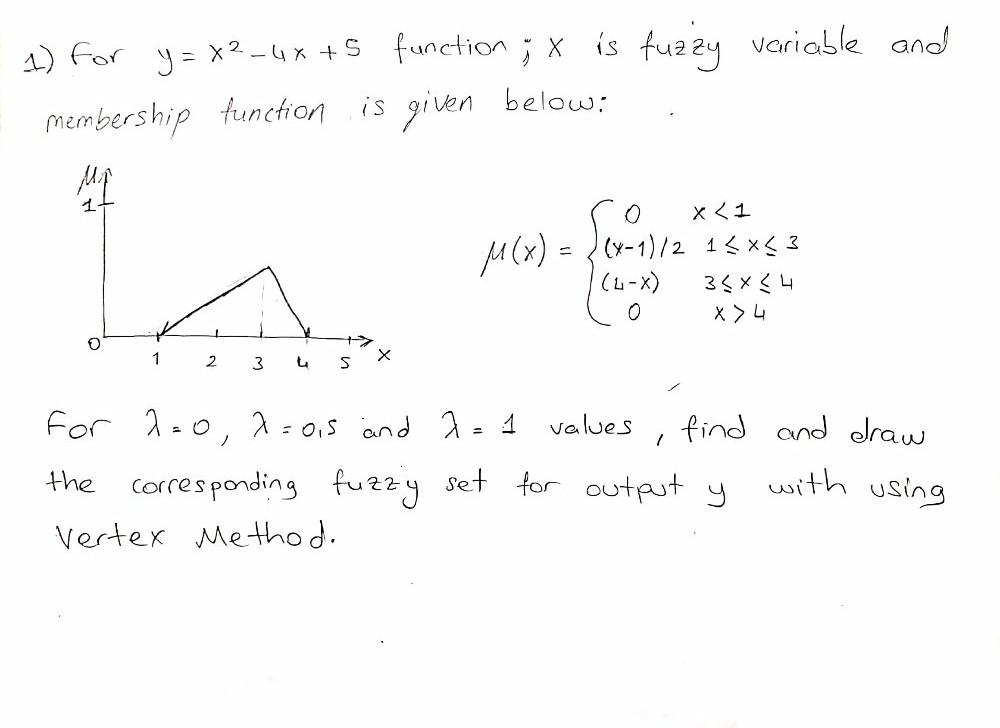
Solved 1 For Y X2 4x 5 Function X Is Fuzzy Variable And Chegg Com

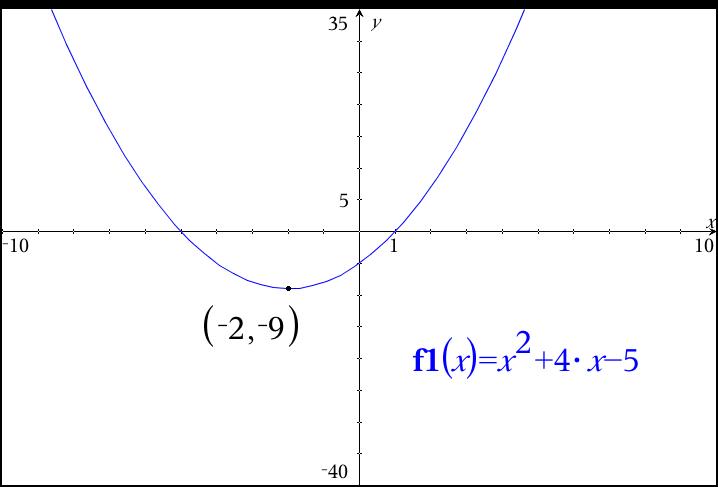
What Is The Vertex Of F X X 2 4x 5 Socratic

Solved Graph Each Parabola And Give Its Vertex Axis Of Chegg Com

X2 4x 5 0 By Quadratic Formula

What Is The Vertex Of Y X 4x 5 Quora

Solution F X X 2 4x 5 Graph The Function Using Its Vertex Axis Of Symmetry And Intercepts

How Do You Find The Vertex Of F X 2x 2 4x 6 Socratic

Solved Graph F X X 2 4x 5 Find The X Intercepts Chegg Com

What Is The Vertex Form Of Y X 2 5x 14 Socratic

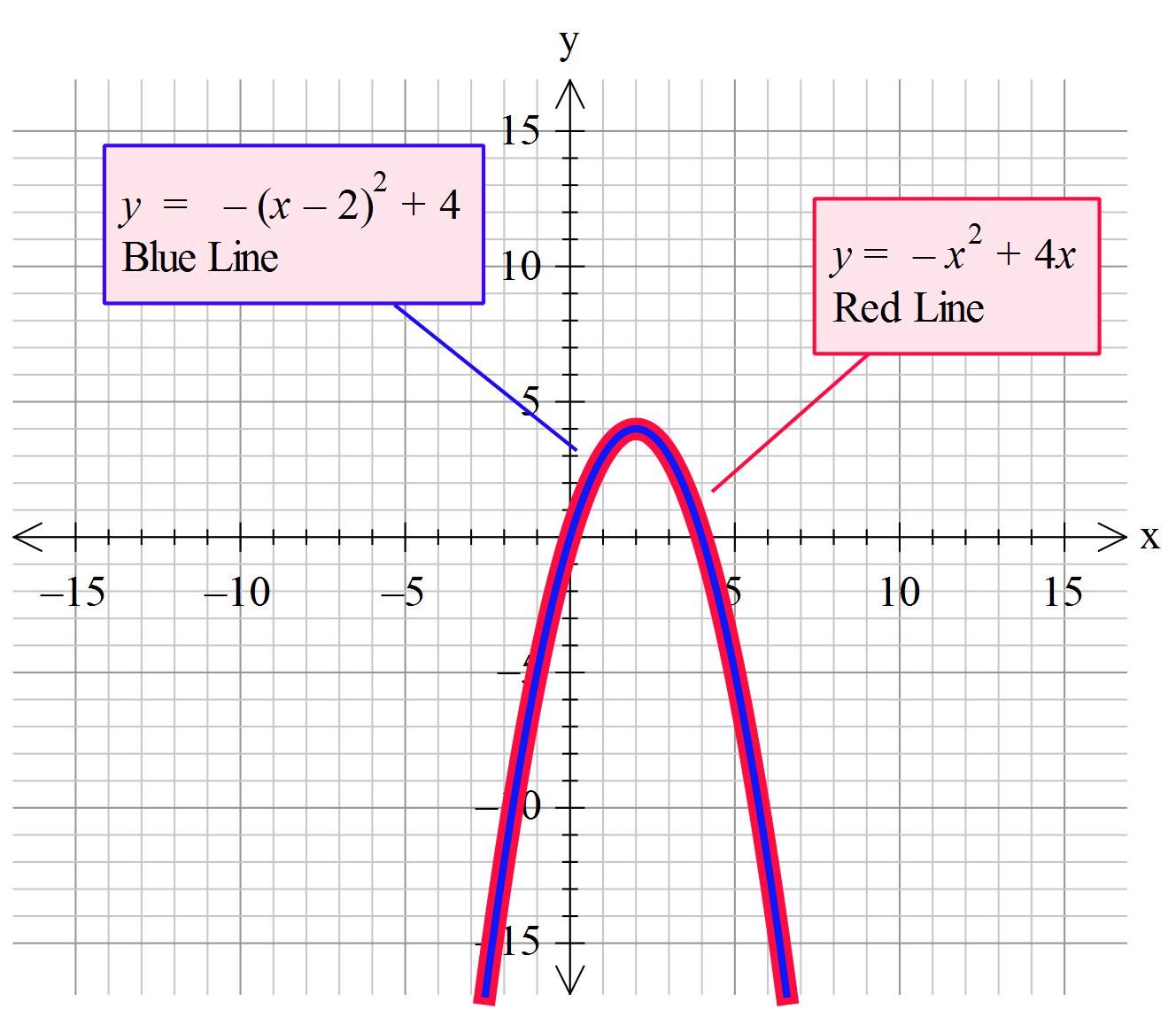
How Do You Write F X X 2 4x In Vertex Form Socratic

What Is The Vertex Of F X X 2 4x 5 Homeworklib

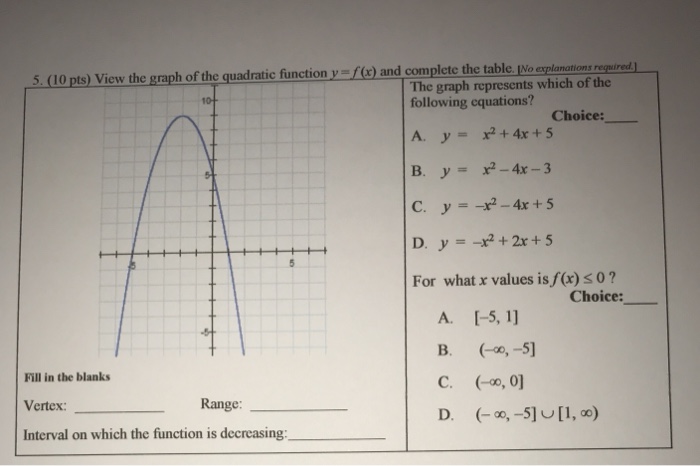
Solved 0 Pts View The Graph Of The Quadratic Function Y F Chegg Com

Parabolas

How To Find Quadratic Line Of Symmetry

A Sketch The Graph Of The Function Y X 2 4x B Find Its Vertex Y Intercept And X Intercepts Study Com

Quadratics

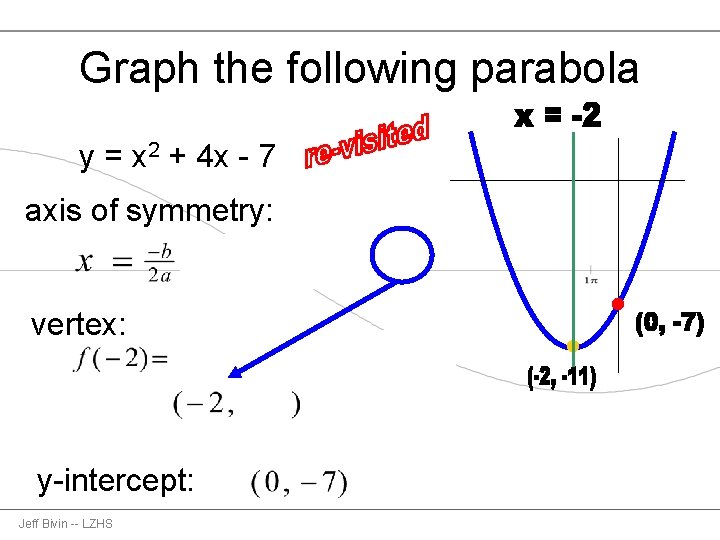
Graphing Parabolas Using The Vertex Axis Of Symmetry

Learn How To Convert To Vertex Form By Completing The Square And Then Graph Y X 2 4x 7 Youtube

Solved Consider The Quadratic Function F X X 2 4x 5 Chegg Com

Consider The Function F X 2 X 2 Ppt Video Online Download

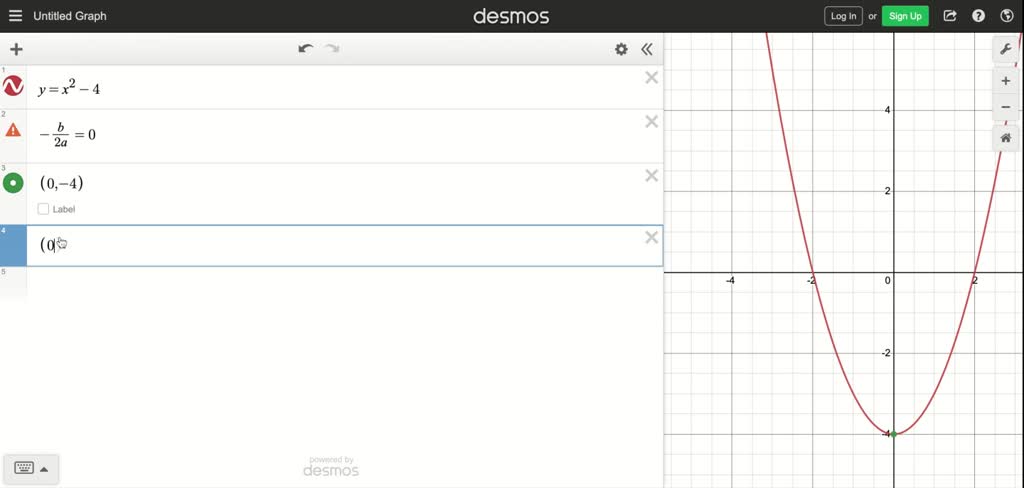
Solved Sketch The Graph Of The Quadratic Function F X X2 4x 4 Selection Tool Line Ray Segment Circle Vertical Parabola Horizontal Parabola Point No Solution Help 10 9 8 7 6 5 4 3 2 10 9 8 7 6 5 4 3 2 Clear Graph Delete

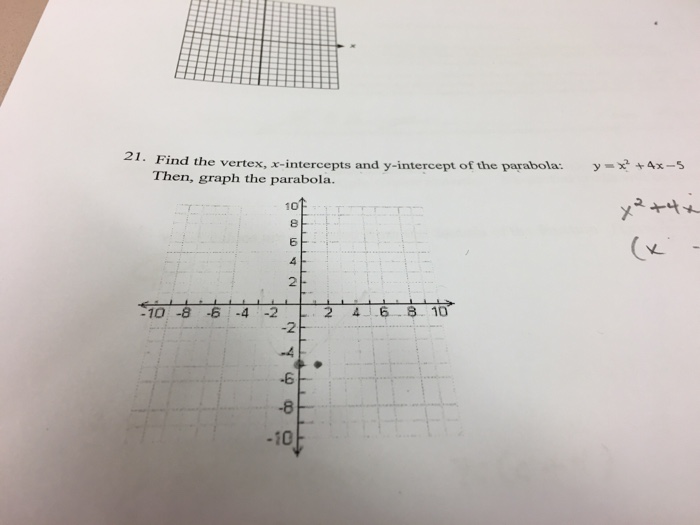
Solved Find The Vertex X Intercepts And Y Intercept Of The Chegg Com